2진 탐색 트리(Binary Search Tree:BST) 구현
Table of contents
트리 자료구조의 간단한 설명
트리 구조는 말 그대로 나무 모양의 데이터 자료구조이고,
리스트나 배열처럼 나열하는 구조가 아닌, 계층 관계를 갖는다.
- 노드 : 하나의 데이터
- 루트 : 트리의 가장 윗 부분에 해당하는 노드
- 리프 : 노드가 더 이상 뻗어나가지 않는 노드 ( 자식 노드를 갖고 있지 않는 노드)
이진 트리는, 노드가 왼쪽, 오른쪽 자식 노드, 즉 2개의 자식 노드를 갖는 트리 구조를 말한다.
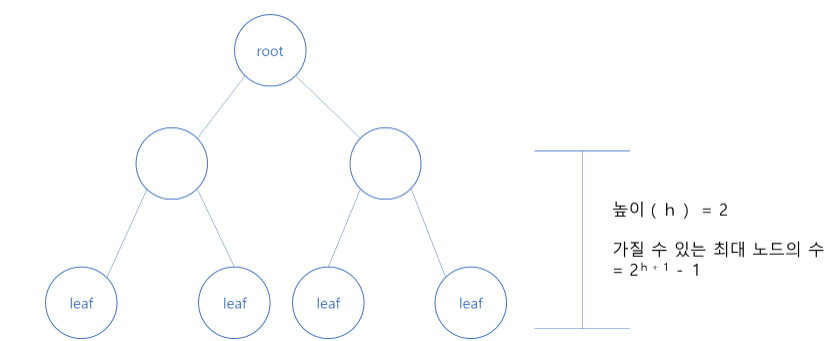
위 그림 처럼 제일 상단에 있는 노드가 root 그리고 더 이상 자식 노드를 갖지 않는 노드들을 leaf라 한다.
왼쪽 자식 노드는 부모 노드보다 작은 값들로만 채워지고, 오른쪽 자식 노드들은 부모 노드보다 큰 값으로 채워진다.
트리구조의 장점은, 구간합을 구하거나, 중간 데이터가 새로 갱신되는 상황에서 시간복잡도가 매우 낮다는 장점이 있다.
그리고, 아직 자료구조와 복잡도에 대해 잘은 모르지만, 트리 구조는 알고리즘 문제를 풀 때, 많이 쓰인다고 한다. (더 알게되는 지식이 생기면 게시글 업데이트를 하겠다.)
Java로 구현하기
먼저, 이진트리를 구현하기 위해서 노드 객체를 정의해야 한다.
각 노드는, 자신의 주소값을 의미하는 key 변수와 노드가 보유하고 있는 data 변수가 필요하다.
또한, 오른쪽 자식 노드, 왼쪽 자식 노드를 참조해야 하므로 노드 객체 2개가 추가로 필요하다.
만약 자식이 없다면 해당 변수 값은 null이 될 것이다.
참고로, 트리 구조의 기준은 Key를 기준으로 노드를 생성한다.
import java.util.Comparator;
//2진 트리 구현
public class BinTree<K, V> {
static class Node<K,V>{
K key; //임의의 자료형 K 타입의 키
V data; // 임의의 자료형 V 타입의 데이터
Node<K,V> left; // 왼쪽 노드 객체
Node<K,V> right; //오른쪽 노드 객체
//1. 노드 생성 시 , 생성자를 사용해서 정보 입력.
public Node(K key, V data, Node<K, V> left, Node<K, V> right) {
this.key = key;
this.data = data;
this.left = left;
this.right = right;
}
//노드의 주소 값 반환, 노드 검색 시 사용됨
public K getKey() {
return key;
}
//노드가 가진 데이터 반환
public V getValue() {
return data;
}
//노드가 가진 데이터 출력
void print() {
System.out.println(data);
}
}
private Node<K,V> root; //트리의 제일 상단에 있는 노드 객체
private Comparator<? super K> comparator = null; //비교자를 명시적으로 설정하지 않으면 null값
public BinTree(){ //비교자를 null(default) 값으로 받는 기본 생성자
root = null;
}
// 비교자를 매개변수로 받는 생성자, customComparator를 받을 수 있다.
public BinTree(Comparator<? super K> c){
this();
comparator = c;
}
}
이진 트리 BinTree 객체는 노드 타입의 root 객체와Comparator 객체 맴버를 갖고 있고, 생성자가 오버로딩 되어있어, 원하는 방식으로 사용하면 된다. 비교자를 따로 명시하지 않는 경우, 우리가 아는 Integer나 String의 대소비교를 수행하게 되고, 새로운 비교 기준을 제공하고 싶은 경우 Comparator 를 매개변수로 Bintree를 생성하면 된다.
//키 값의 대소비교
private int comp(K key1, K key2){
return (comparator == null)?((Comparable<K>key1)).compareTo(key2):comparator.compare(key1,key2);
}
comp() 메서드는, 키 값을 비교하는 메서드로, 데이터를 추가할 때 왼쪽 자식 노드로 보내야 할지, 오른쪽 노드로 보내야할지 선택하는 작업 등에 사용된다.
comparator 가 null 이라는 뜻은, 따로 comparator을 제공하지 않았다는 의미이므로 K 타입의 key를 기존의 Comparable 인터페이스의 compareTo메서드를 사용하기 위해서 형 변환을 시켜준뒤 compareTo를 하면 된다.
Comparator를 제공한 경우, 오버라이딩 한 compare메서드를 사용하도록 구현하면 된다.
// K key 를 기준으로 V data를 반환하는 메서드
public V search(K key){
Node<K,V> p = root; //루트(최상단 노드)
while(true){
if(p == null) { //최상단 노드가 null이라면 검색할 것이 없음.
return null;
}
int cond = comp(key,p.getKey());
if(cond == 0){ //comp() 결과가 0이라는 뜻은, 해당 key에 해당하는 노드라는 것
return p.getValue();
}
else if(cond < 0){
p = p.left; //0보다 작다는 뜻은 비교한 키의 왼쪽 자식 노드 방향으로 가야한다는 의미
}
else{
p = p.right; //0보다 크다는 뜻은 비교한 키의 오른쪽 자식 노드 방향으로 가야한다는 의미
}
}
}
serach() 메서드는 매개변수로 입력되는 K key에 해당하는 V data를 반환하는 메서드이다. 먼저, 트리의 최상단인 root 에서 시작한다.
만약 p==null 이라는 의미는 어떠한 key 와 data 가 채워져 있지 않은 트리 이므로 null 을 반환한다.
null이 아니라면, 최상단 root의 key 값과 매개변수로 넣은 key 값을 비교한다.
comp(key,p,getKey()) 값이 0 이라면, 검색에 성공한 것이고,
음수라면 매개변수로 입력한 key가 작다는 의미이므로 왼쪽 자식 노드(left)로 이동해야하고,
양수라면, 입력한 key가 더 크다는 의미이므로 오른쪽 자식 노드(right)로 이동해야 할 것이다.
따라서, root에서 시작한 node객체 p에 p.left 또는 p.right로 갱신해준다.
갱신된 객체의 key값과 매개변수로 입력한 key값의 대소비교가 또 이루어질 것이다.
결국, while(true) 문에 의해 comp() 반환값이 0이 될때 까지 수행될 것이다.
//적절한 위치에 Node 객체를 생성하는 메서드
private void addNode(Node<K,V> node, K key , V data){
int cond = comp(key,node.getKey());
if(cond == 0){ //매개변수로 넣은 key값 과의 대소비교에서 0이라는 의미는 이미 존재한다는 뜻
return;
}
else if(cond <0){// 왼쪽 자식 노드로 이동
if(node.left == null){ //아직 왼쪽 자식 노드가 비어있다면 노드 등록
node.left = new Node<K,V>(key, data, null, null);
}
else{
addNode(node.left, key, data); //왼쪽 노드 객체를 기준으로 key값 한번 더 key 비교
}
}
else{
if(node.right == null){ //아직 오른쪽 자식 노드가 비어있다면 노드 등록
node.right = new Node<K,V>(key, data, null, null);
}
else{
addNode(node.right, key, data); //왼쪽 노드 객체를 기준으로 key값 한번 더 key 비교
}
}
}
//노드 삽입 메서드
public void add(K key, V data){
if(root == null){//아직 최상단 노드인 루트가 비어있다면 생성자로 할당
root = new Node<K,V>(key, data, null, null);
}
else{
addNode(root, key, data);
}
}
addNode는 트리 구조에 key값을 비교하여 적절한 위치에 노드 객체를 생성하고 맴버 변수에 데이터를 기록하는 메서드이다.
만약 comp(key, node.getKey()) 값이 0이라는 의미는 key값이 같다는 의미이므로, 이미 존재하는 데이터임을 알 수 있다. 따라서 아무런 작업이 이뤄지지 않는다.
0보다 작다면, 왼쪽 자식 노드로 가서 비교해봐야 할 것이다. 만약 아직 왼쪽 자식 노드가 null값으로 생성되지 않는 경우라면 그 위치에다 객체를 생성하면 된다.
그렇지 않은 경우라면, 재귀호출을 통해서 비교 작업을 계속 해야한다.
comp()값이 0보다 큰 경우도 마찬가지로 진행된다.
//key 값에 해당하는 노드 삭제
public boolean remove(K key) {
Node<K, V> p = root; //최상단 root 노드에서 시작
Node<K, V> parent = null; // 최상단 root 노드의 부모 노드는 없다.
boolean isLeftChild = true; //찾으려는 노드가 왼쪽에 있는지 확인하는 boolean
while (true) {
if (p == null) { //데이터가 존재하지 않는 곳까지 이동하면 매개변수로 입력한 key 값이 없다는 의미이므로 false 반환
return false;
}
int cond = comp(key, p.getKey()); //찾으려는 키(key)와 지금 위치(p.getKey())의 키를 비교
if (cond == 0) {
break; // 찾았으면 p 가 삭제하려는 키를 가리키고 있을 것 그러므로 루프 종료
} else { //못찾은 경우
parent = p; //부모 노드로 지금 위치를 지정
if (cond < 0) { //찾으려는 키(p.getKey())가 지금 키(key)보다 작은 경우, 왼쪽으로 가야함
isLeftChild = true; //왼쪽 자식 노드로 가야하므로 true;
p = p.left; //비교 대상 노드를 p의 왼쪽 자식 노드로 갱신
} else { //찾으려는 데이터가 지금 위치보다 큰 경우
isLeftChild = false; //오른쪽 노드로 가야하므로 false;
p = p.right; //비교 대상 노드를 오른쪽 자식 노드로 갱신
}
}
}
// 위 루프를 통해서 결과적으로, 찾으려는 키의 객체를 갖고옴
if (p.left == null) { //찾은 객체의 왼쪽 자식 노드가 없는 경우
if (p == root) { //찾은 객체가 최상단 노드인 root인 경우
root = p.right;
//그리고 그 최상단 루트가 왼쪽 자식이 없다면,
//최상단 노드인 root를 오른쪽 자식 주소로 갱신만 해주면 됨
}
else if (isLeftChild) { //위 루프를 통해 찾은 키의 객체, 즉 지우려고 하는 객체가 부모의 왼쪽 자식 노드인 경우
parent.left = p.right;
// 검색한 p의 노드는 지워야 하기때문에 그리고 p는 왼쪽 노드가 없기 때문에,
// 부모의 왼쪽 자식 노드를 p의 오른쪽 자식 노드 값으로 갱신만 해주면 성립된다. (그림 그려보면 이해 잘됨)
}
else {
parent.right = p.right;
// 만약 부모의 오른쪽 자식 노드라면
// 검색한 p의 위치는 지워야 하기때문에 그리고 p는 왼쪽 노드가 없기 때문에,
// 부모의 오른쪽 노드를 p의 오른쪽 노드 값으로 갱신만 해주면 됨
}
}
else if (p.right == null) {
//만약 검색한 노드의 오른쪽 자식이 없다면? 위 과정과 비슷하다.
if (p == root) {
root = p.left;
}
else if (isLeftChild) {
parent.left = p.left;
}
else {
parent.right = p.left;
}
}
else {//검색한 노드가 왼쪽 오른쪽 자식 둘다 있는 경우, 제거하기 위해서
//키보다 작은 키들 중 가장 최댓값 키를 찾아서 집어넣고, 그 최댓값 키의 부모 노드에는
//찾은 최댓값 키의 자식 노드를 넘겨주고 가야함
//최댓값이라 하면 검색한 노드의 왼쪽에서 출발하여 가장 오른쪽 가지에 있는 것
parent = p;
Node<K, V> left = p.left; //제거하려는 p의 왼쪽 자식 노드 객체 생성
isLeftChild = true;
while (left.right != null) { //자식 노드의 오른쪽 자식이 없을 때 까지의 의미는, 왼쪽 노드 중 최댓값을 의미
parent = left;
left = left.right;
isLeftChild = false;
}
//위 루프를 통해, 가장 오른쪽 자식이 없는 노드를 검색 완료
// (left에 삭제할 노드 다음으로 큰 값이 저장될 것)
p.key = left.key; //삭제할 p 객체의 맴버를 위 루프를 통해 구한 left 객체의 맴버로 전부 변환
p.data = left.data;
if (isLeftChild) { //
parent.left = left.left;
//부모의 왼쪽 노드 주소를 검색한 left
} else {
parent.right = left.left;
}
}
return true;
}
remove 메서드는 입력한 key에 해당하는 노드를 지우는 메서드이다.
remove 메서드 역시 최상단 노드인 root에서 시작한다.
첫번째 while루프문을 통해서 매개변수로 입력한 key에 해당하는 node p를 찾는다.
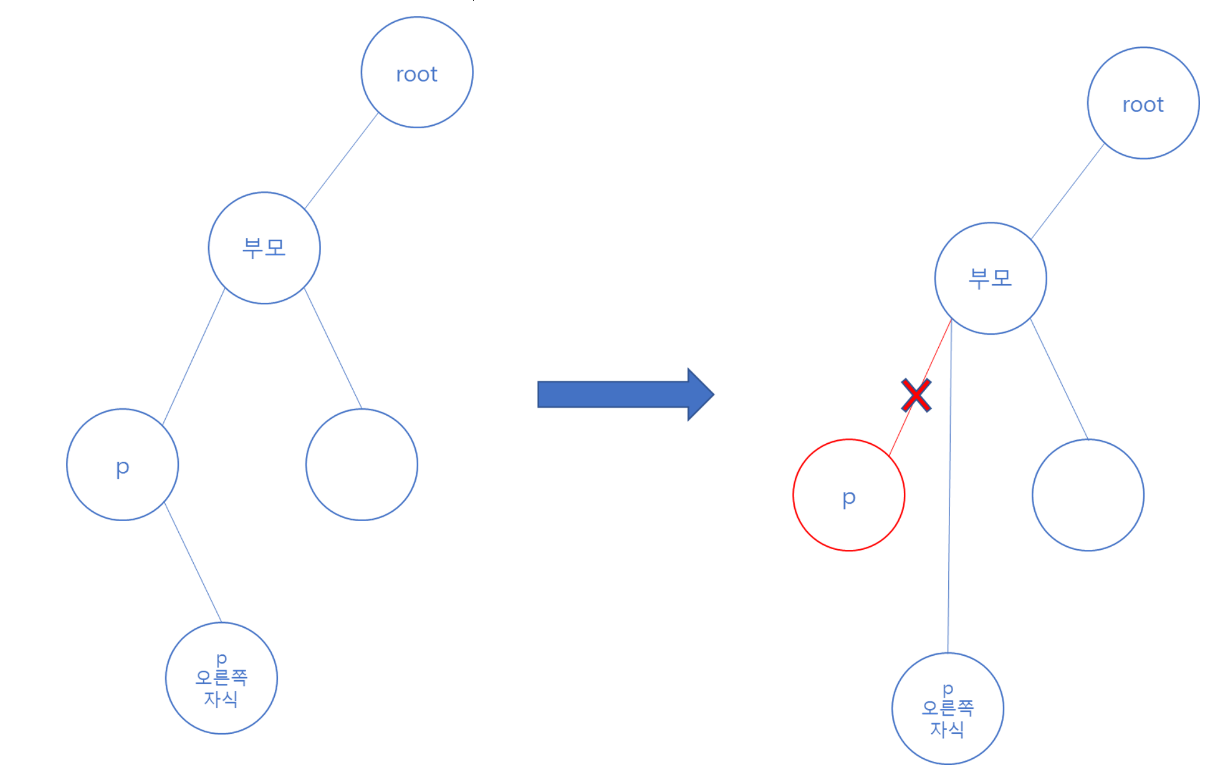
찾은 p(제거하려는 노드)의 왼쪽 자식 노드가 없고, p가 부모의 왼쪽 자식 노드라면(isLeftChild값이 true인 경우)
부모의 왼쪽 자식 노드를 p의 오른쪽 자식 노드로 넘겨주면 된다.
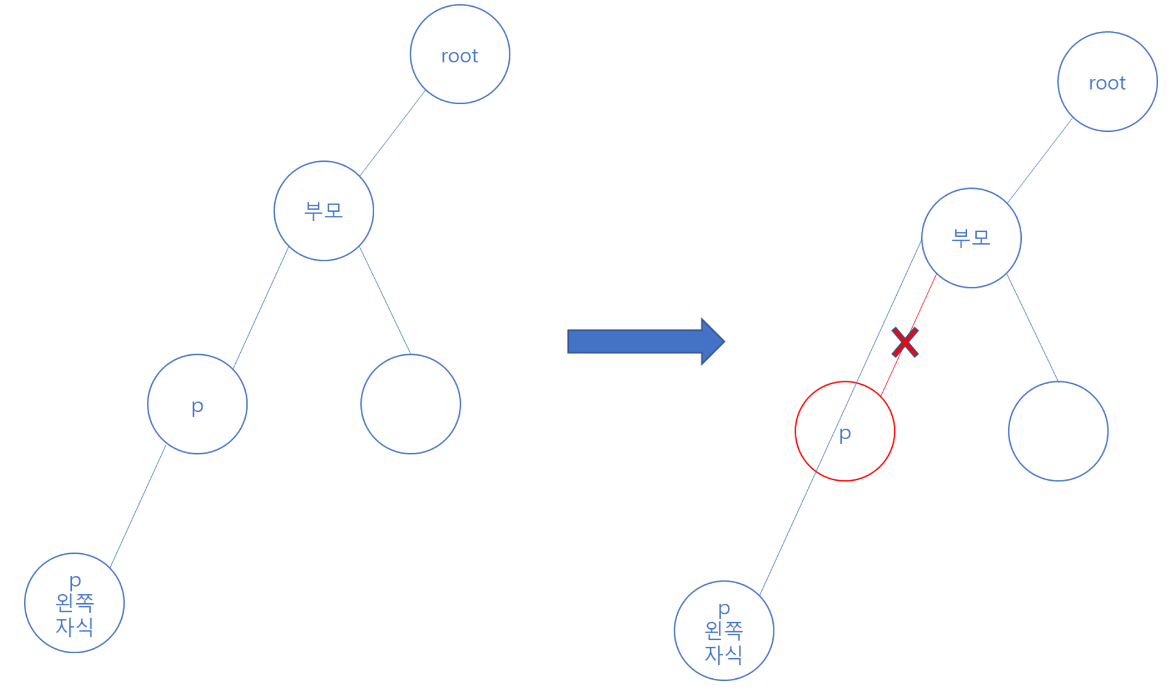
찾은 p의 오른쪽 자식 노드가 없고, p가 부모의 왼쪽 자식 노드라면
부모의 왼쪽 자식 노드를 p의 왼쪽 자식 노드로 넘겨주면 된다.
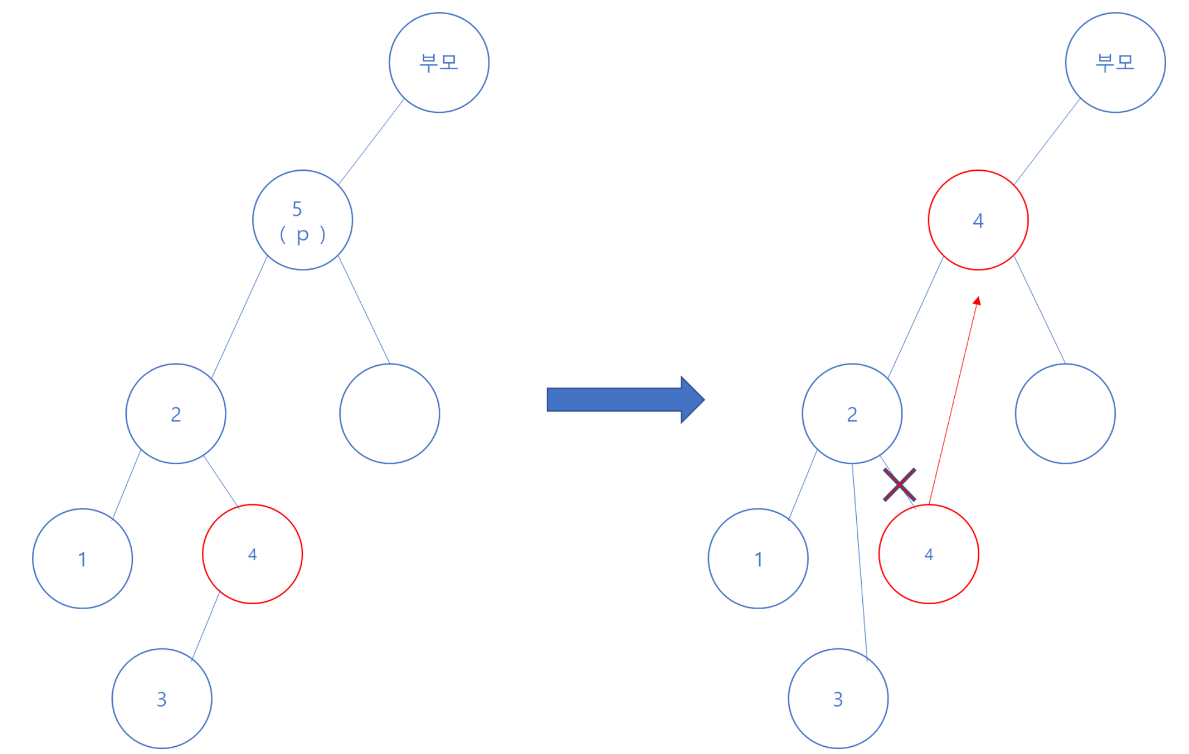
제거하려는 p가 자식이 2개 다 있다면, 조금 까다로운데
먼저 제거하려는 p보다 작은 key 값들 중 가장 큰 key 값을 찾아서 제거하려는 p 노드 위치에 넣어주고
자식 노드는 옮긴 노드의 부모 노드에 그대로 연결시켜주어야 한다. 참고로 옮기려는 노드의 오른쪽 자식은 있을 수 없다.
왜냐하면, 오른쪽 자식이 없는 노드가 제거하려는 p노드보다 작은 노드 중 최댓값이기 때문이다.
완성 코드
import java.util.Comparator;
//2진 트리 구현
public class BinTree<K, V> {
static class Node<K,V>{
K key; //임의의 자료형 K 타입의 키
V data; // 임의의 자료형 V 타입의 데이터
Node<K,V> left; // 왼쪽 노드 객체
Node<K,V> right; //오른쪽 노드 객체
//1. 노드 생성 시 , 생성자를 사용해서 정보 입력.
public Node(K key, V data, Node<K, V> left, Node<K, V> right) {
this.key = key;
this.data = data;
this.left = left;
this.right = right;
}
//노드의 주소 값 반환, 노드 검색 시 사용됨
public K getKey() {
return key;
}
//노드가 가진 데이터 반환
public V getValue() {
return data;
}
//노드가 가진 데이터 출력
void print() {
System.out.println(data);
}
}
private Node<K,V> root; //트리의 제일 상단에 있는 노드 객체
private Comparator<? super K> comparator = null; //비교자를 명시적으로 설정하지 않으면 null값
public BinTree(){ //비교자를 null(default) 값으로 받는 기본 생성자
root = null;
}
// 비교자를 매개변수로 받는 생성자, customComparator를 받을 수 있다.
public BinTree(Comparator<? super K> c){
this();
comparator = c;
}
//키 값의 대소비교
private int comp(K key1, K key2){
return (comparator == null)?((Comparable<K>key1)).compareTo(key2):comparator.compare(key1,key2);
}
// K key 를 기준으로 V data를 반환하는 메서드
public V search(K key){
Node<K,V> p = root; //루트(최상단 노드)
while(true){
if(p == null) { //최상단 노드가 null이라면 검색할 것이 없음.
return null;
}
int cond = comp(key,p.getKey());
if(cond == 0){ //comp() 결과가 0이라는 뜻은, 해당 key에 해당하는 노드라는 것
return p.getValue();
}
else if(cond < 0){
p = p.left; //0보다 작다는 뜻은 비교한 키의 왼쪽 자식 노드 방향으로 가야한다는 의미
}
else{
p = p.right; //0보다 크다는 뜻은 비교한 키의 오른쪽 자식 노드 방향으로 가야한다는 의미
}
}
}
//적절한 위치에 Node 객체를 생성하는 메서드
private void addNode(Node<K,V> node, K key , V data){
int cond = comp(key,node.getKey());
if(cond == 0){ //매개변수로 넣은 key값 과의 대소비교에서 0이라는 의미는 이미 존재한다는 뜻
return;
}
else if(cond <0){// 왼쪽 자식 노드로 이동
if(node.left == null){ //아직 왼쪽 자식 노드가 비어있다면 노드 등록
node.left = new Node<K,V>(key, data, null, null);
}
else{
addNode(node.left, key, data); //왼쪽 노드 객체를 기준으로 key값 한번 더 key 비교
}
}
else{
if(node.right == null){ //아직 오른쪽 자식 노드가 비어있다면 노드 등록
node.right = new Node<K,V>(key, data, null, null);
}
else{
addNode(node.right, key, data); //왼쪽 노드 객체를 기준으로 key값 한번 더 key 비교
}
}
}
//노드 삽입 메서드
public void add(K key, V data){
if(root == null){//아직 최상단 노드인 루트가 비어있다면 생성자로 할당
root = new Node<K,V>(key, data, null, null);
}
else{
addNode(root, key, data);
}
}
//key 값에 해당하는 노드 삭제
public boolean remove(K key) {
Node<K, V> p = root; //최상단 root 노드에서 시작
Node<K, V> parent = null; // 최상단 root 노드의 부모 노드는 없다.
boolean isLeftChild = true; //찾으려는 노드가 왼쪽에 있는지 확인하는 boolean
while (true) {
if (p == null) { //데이터가 존재하지 않는 곳까지 이동하면 매개변수로 입력한 key 값이 없다는 의미이므로 false 반환
return false;
}
int cond = comp(key, p.getKey()); //찾으려는 키(key)와 지금 위치(p.getKey())의 키를 비교
if (cond == 0) {
break; // 찾았으면 p 가 삭제하려는 키를 가리키고 있을 것 그러므로 루프 종료
} else { //못찾은 경우
parent = p; //부모 노드로 지금 위치를 지정
if (cond < 0) { //찾으려는 키(p.getKey())가 지금 키(key)보다 작은 경우, 왼쪽으로 가야함
isLeftChild = true; //왼쪽 자식 노드로 가야하므로 true;
p = p.left; //비교 대상 노드를 p의 왼쪽 자식 노드로 갱신
} else { //찾으려는 데이터가 지금 위치보다 큰 경우
isLeftChild = false; //오른쪽 노드로 가야하므로 false;
p = p.right; //비교 대상 노드를 오른쪽 자식 노드로 갱신
}
}
}
// 위 루프를 통해서 결과적으로, 찾으려는 키의 객체를 갖고옴
if (p.left == null) { //찾은 객체의 왼쪽 자식 노드가 없는 경우
if (p == root) { //찾은 객체가 최상단 노드인 root인 경우
root = p.right;
//그리고 그 최상단 루트가 왼쪽 자식이 없다면,
//최상단 노드인 root를 오른쪽 자식 주소로 갱신만 해주면 됨
}
else if (isLeftChild) { //위 루프를 통해 찾은 키의 객체, 즉 지우려고 하는 객체가 부모의 왼쪽 자식 노드인 경우
parent.left = p.right;
// 검색한 p의 노드는 지워야 하기때문에 그리고 p는 왼쪽 노드가 없기 때문에,
// 부모의 왼쪽 자식 노드를 p의 오른쪽 자식 노드 값으로 갱신만 해주면 성립된다. (그림 그려보면 이해 잘됨)
}
else {
parent.right = p.right;
// 만약 부모의 오른쪽 자식 노드라면
// 검색한 p의 위치는 지워야 하기때문에 그리고 p는 왼쪽 노드가 없기 때문에,
// 부모의 오른쪽 노드를 p의 오른쪽 노드 값으로 갱신만 해주면 됨
}
}
else if (p.right == null) {
//만약 검색한 노드의 오른쪽 자식이 없다면? 위 과정과 비슷하다.
if (p == root) {
root = p.left;
}
else if (isLeftChild) {
parent.left = p.left;
}
else {
parent.right = p.left;
}
}
else {//검색한 노드가 왼쪽 오른쪽 자식 둘다 있는 경우, 제거하기 위해서
//키보다 작은 키들 중 가장 최댓값 키를 찾아서 집어넣고, 그 최댓값 키의 부모 노드에는
//찾은 최댓값 키의 자식 노드를 넘겨주고 가야함
//최댓값이라 하면 검색한 노드의 왼쪽에서 출발하여 가장 오른쪽 가지에 있는 것
parent = p;
Node<K, V> left = p.left; //제거하려는 p의 왼쪽 자식 노드 객체 생성
isLeftChild = true;
while (left.right != null) { //자식 노드의 오른쪽 자식이 없을 때 까지의 의미는, 왼쪽 노드 중 최댓값을 의미
parent = left;
left = left.right;
isLeftChild = false;
}
//위 루프를 통해, 가장 오른쪽 자식이 없는 노드를 검색 완료
// (left에 삭제할 노드 다음으로 큰 값이 저장될 것)
p.key = left.key; //삭제할 p 객체의 맴버를 위 루프를 통해 구한 left 객체의 맴버로 전부 변환
p.data = left.data;
if (isLeftChild) { //
parent.left = left.left;
//부모의 왼쪽 노드 주소를 검색한 left
} else {
parent.right = left.left;
}
}
return true;
}
//트리 출력하는 메서드
private void printSubTree(Node node) {
if (node != null) {
printSubTree(node.left);
System.out.println(node.key + " " + node.data);
printSubTree(node.right);
}
}
public void print(){
printSubTree(root);
}
}