세그먼트 트리 구현
이진 탐색 트리는, Key 값과 Data 값 두개를 갖고, Key 값을 기준으로 정렬하는 트리구조였다.
세그먼트 트리는, 이진 탐색 트리와 비교했을 때는, Key 값만 갖는 조금 더 단순한 구조이다. 또한, Node 객체를 정의해서 사용하는 것이 아닌, 배열 하나로 구성할 수 있다. 배열의 구간합이나, 값의 변경을 빠른 시간안에 해결을 요구하는 문제에서 사용하기 좋은 자료구조이다.
static class SegmentTree {
//트리 데이터를 저장할 배열
long [] tree;
SegmentTree(long [] arr) {
//트리 높이 계산
//Math.log 는 밑이 10인 자연로그 이므로 Math.log(2) 로 한번 더 나누어준다.
// 구간합을 나타내는 세그먼트 트리의 경우 높이는 (log2(N))을 올림한 값이 된다. (예시로 설명 가능)
int arrSize = arr.length;
int h = (int) Math.ceil(Math.log(arrSize) / Math.log(2));
//트리 노드 수 계산
int treeSize = (int) Math.pow(2, h + 1);
//트리사이즈로 트리 생성하고 입력된 배열로 초기 트리 생성
tree = new long[treeSize];
init(arr,1,0,arrSize-1);
}
}
먼저, 트리 구조로 원소를 저장할 배열을 long [] tree 변수를 선언하고, 생성자를 통해서 초기화된다.
트리구조로 변경할 배열을 매개변수를 가진 생성자를 통해서 입력받는다.
그리고 입력받은 배열의 길이를 통해서, 트리의 높이를 결정할 수 있다.
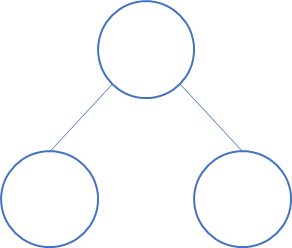
입력받은 원소의 갯수가 1~2개일 때, 구간합은 최대 1개만 나오므로 높이는 1이 되고
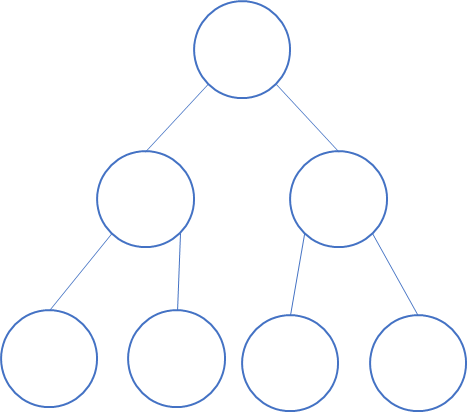
입력받은 원소의 갯수가 3~4개일 때, 구간합이 최대 3개가 나오므로, 높이는 2가 되고
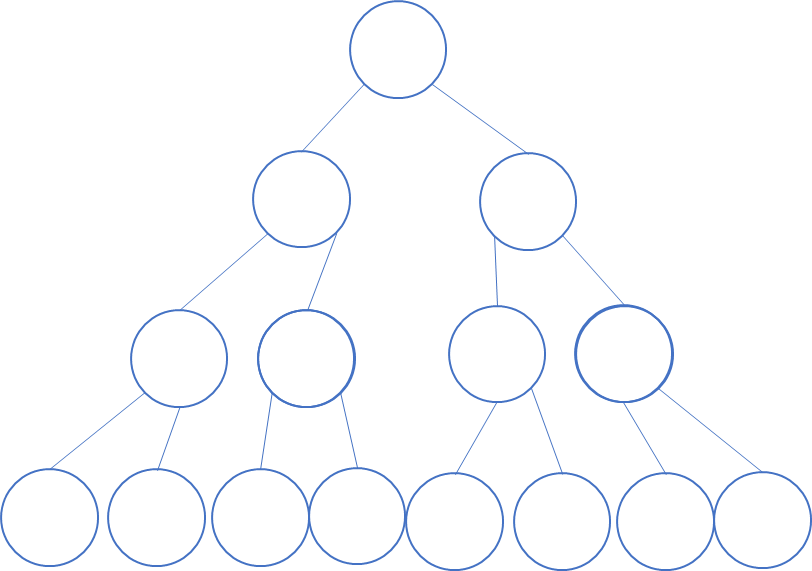
입력받은 원소의 갯수가 5~8개일 때, 구간합이 최대 7개가 나오므로, 높이는 3이 된다.
따라서 높이는 log2(원소의 갯수)를 올림한 값으로 설정하면, 충분한 저장공간을 생성할 수 있다.
노드 수는 위 과정을 통해 설정한 트리의 높이로 treesize = 2^(h+1) 와 같이 결정할 수 있다.
그렇게 tree배열을 생성하고 init 메서드로 초기 트리를 생성한다.
long init(long[] arr, int nodeIndex, int start, int end) {
if (start == end) { //같아지는 순간 데이터를 집어 넣는다.
return tree[nodeIndex] = arr[start];
} else { // 리프 노드를 제외한 노드에는 아래 구문에 의해, 구간 합이 저장될 것이다.
int midPoint = (start+end)/2;
return tree[nodeIndex] =
init(arr, nodeIndex * 2, start, midPoint)
+ init(arr, nodeIndex * 2 + 1, midPoint + 1, end);
}
}
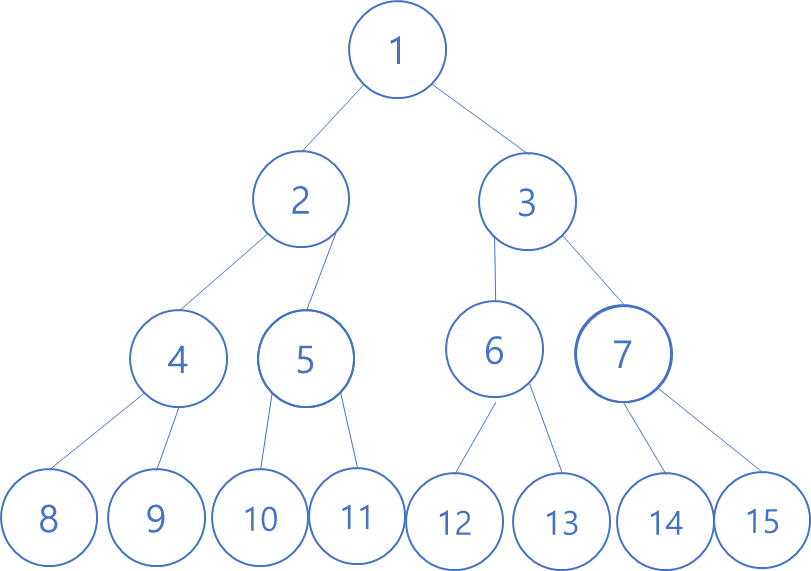
트리 구조를 만들기 위한 작업, 재귀식 작업이다. 리프 노드일 때까지(자식 노드를 가지지 않는)진행된다. 리프 노드에 배열로 전달된 값들을 넣고, 부모 노드에는 구간 합을 삽입하는 방식이다.
root 노드의 경우 인덱스 1, root 노드의 왼쪽 자식은 인덱스 2, 오른쪽 자식은 3이 된다.
root의 왼쪽자식의 왼쪽 자식은 2x2=4 , 왼쪽 자식의 오른쪽 자식은 2x2 +1 = 5,
root의 오른쪽 자식의 왼쪽자식은 3x2=6 , 오른쪽 자식의 오른쪽 자식은 3x2+1 = 7
즉, 부모 인덱스가 i 라면 왼쪽 자식 인덱스는 ix2 , 오른쪽 자식 인덱스는 2xi+1이라는 결론을 내릴 수 있다.
void update(int nodeIndex, int start, int end, int index, int diff) {
if (index < start || index > end) {
return ;
}
tree[nodeIndex] += diff;
if (start != end) {
int midPoint = (start + end) / 2;
update(nodeIndex * 2, start, midPoint, index, diff);
update(nodeIndex * 2 + 1, midPoint + 1, end, index, diff);
}
}
update 메서드는 배열의 원소가 변경되었을 때, 트리구조에 반영하는 메서드이다. 바꾸려는 데이터를 포함해서, 그 데이터가 포함되어있던 구간합에 값 차이를 더해주면 된다.
nodeIndex 는 루트 노드 인덱스인 1 을 넣어주면 되고,
start 와 end 는 트리구조의 배열이 아닌, 트리구조로 만들기 전 배열의 시작 인덱스와 끝 인덱스를 넣으면 되고,
index 는 트리구조로 만들기 전 배열의 변경하고자 하는 인덱스를 입력하면 된다.
diff는 변경하고자 하는 값과 원래 값의 차이를 입력하면 된다. 만약 1L 에서 3L 로 변경하고자 한다면 diff 값을 +2L 을 입력하면 된다.
long sum(int nodeIndex, int start, int end, int left, int right) {
// 범위를 벗어나게 되는 경우 더할 필요 없음
if (right < start || left > end) {
return 0;
}
// 범위 내 완전히 포함 시에는 더 내려가지 않고 바로 리턴
//left 랑 right 는 우리가 구하고자 하는 구간이라 고정
//start~end 는 구간합 즉 left<+start ~ end<=right 를 만족하면 값을 반환하면 됨
if (left <= start && end <= right) {
return tree[nodeIndex];
}
// 그 외의 경우 좌 / 우측으로 지속 탐색 수행
int midPoint = (start + end) / 2;
return sum(nodeIndex * 2, start, midPoint, left, right)
+ sum(nodeIndex * 2 + 1, midPoint + 1, end, left, right);
}
구간합 코드도, update코드와 유사한데, left ~ right 는 우리가 구간합을 구하고자 하는 배열의 인덱스 범위이다. 따라서, 값이 변하지는 않고,
start 와 end 만 변하게 된다. left <= start && end <= right 를 만족할때는, 굳이 자식노드로 내려가지 않아도, 구간합을 반환할 수 있기 때문에 return 하도록 되어 있다.
완성 코드
public class SegmentTree {
long tree[];
public SegmentTree(long[] arr) {
int arrSize = arr.length;
int treeHeight = (int) Math.ceil(Math.log(arrSize) / Math.log(2));
int treeSize = (int) Math.pow(2, treeHeight + 1);
tree = new long[treeSize];
init(arr, 1, 0, arrSize - 1);
}
long init(long[] arr, int nodeIndex, int start, int end) {
if (start == end) {
return tree[nodeIndex] = arr[start];
} else {
int midPoint = (start + end) / 2;
return tree[nodeIndex] = init(arr, nodeIndex * 2, start, midPoint)
+ init(arr, nodeIndex * 2 + 1, midPoint + 1, end);
}
}
void update(int nodeIndex, int start, int end, int index, int diff) {
if (index < start || index > end) {
return ;
}
tree[nodeIndex] += diff;
if (start != end) {
int midPoint = (start + end) / 2;
update(nodeIndex * 2, start, midPoint, index, diff);
update(nodeIndex * 2 + 1, midPoint + 1, end, index, diff);
}
}
long sum(int nodeIndex, int start, int end, int left, int right) {
if (right < start || left > end) {
return 0;
}
if (left <= start && end <= right) {
return tree[nodeIndex];
}
int midPoint = (start + end) / 2;
return sum(nodeIndex * 2, start, midPoint, left, right)
+ sum(nodeIndex * 2 + 1, midPoint + 1, end, left, right);
}
}